How to fix statistically misleading pull rate infographics

[pfm]

Crown Zenith dropped and wow! Palkia is rarer than both Pokemon God and Satan. And why is Suicune twice as common as Leafeon?? Something seems amiss…

Hold on one second.

Now 5077 packs might seem like a lot. But we are attempting to quantify the probability of rare events. How many of each card was actually pulled in these 5077 packs? It’s easy to calculate:
pull rate × total packs

Card	Pull Rate*	Decimal	Pulled
Palkia	1/846	0.00118	6
Arceus	1/635	0.00157	8
Dialga	1/423	0.00236	12
Giratina	1/423	0.00236	12
Mewtwo	1/242	0.00413	21
Darkrai	1/423	0.00236	12
Leafeon	1/452	0.00221	11.2[1]
Regigigas	1/423	0.00236	12
Zoroark	1/317	0.00315	16
Suicune	1/203	0.00493	25

So we actually see between 6 and 25 of each card being pulled in this experiment. The infographic would suggest you need 211 more packs (on average) to pull a Palkia compared to an Arceus. But this is based on the difference between 6 and 8 pulls in 5077 packs.

What if by chance we pulled 6 Arceus and 8 Palkia instead? How much of these numbers are real vs entirely due to chance? Fortunately, statistics exists. We can model this experiment after a binomial distribution. This is just a fancy way of “pretending” like we redid this pack-opening experiment many times in order to get an idea of how much variability we should expect in the results.

Details if you are interested.

The binomial distribution with is a probability distribution of the number of successes in a sequence of independent experiments ^[2], each asking a yes–no question, and each with its own outcome: success ^[3] or failure ^[4]

Adapted from Wikipedia - Binomial distribution

Note: this makes an assumption about independent experiments. This is the same thing as saying that you cannot make a prediction about the next pack you open based on the last pack. It’s not a great assumption because if you’ve ever opened a box, you know there’s an expected number of hits. In other words, pulling a gold card in one pack means the chance of the next pack having a gold card is reduced (ie. not independent). There is also an effect with the case of boxes not being independent either. But if you were to buy multiple cases and open all the boxes and shuffled all the packs randomly, it would be more or less independent. Basically it’s not a horrible assumption to make.

---

In this case, we know how many packs have been opened (“trials” or “sample size”) and the number of each hit pulled (“successes”). What we want to find is the true pull rate. Because this experiment is affected by randomness, the can only take a best guess at what the true pull rate is. We can make a 95% confidence interval easily using online tools ^[5].

A 95% confidence interval is just defines a range based on the data we have. It accounts for the randomness in the experiment. Basically, there will be a 95% chance that the true pull rate is somewhere within this range. Let’s do an example:

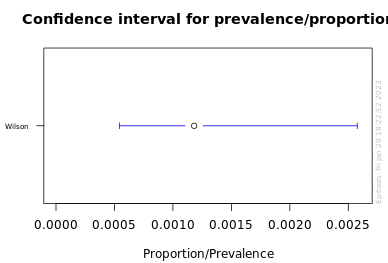
6 Palkia pulled in 5077 packs. Our BEST ESTIMATE of the pull rate is 1/846 (0.00118).
The 95% confidence interval : 0.0005 - 0.0026 ^[6]



This means we are pretty confident that the true pull rate for Palkia is somewhere between 1/2000 and 1/385.

That’s a massive range and the “misleading” part of the infographic. The problem is that while 5077 packs is a lot, it’s not nearly enough to accurately quantify such a rare event.

In contrast consider the “V, VMAX OR VSTAR” rate of 1/15

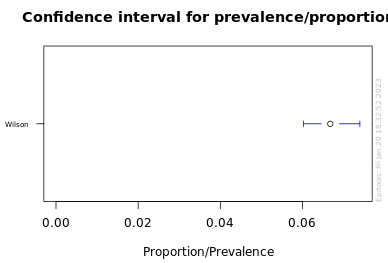
339 V, VMAX OR VSTAR pulled in 5077 packs. Our BEST ESTIMATE of the pull rate is 1/15 (0.067).
The 95% confidence interval : 0.0602 - 0.0740



This means we are pretty confident that the true pull rate for V, VMAX OR VSTAR is somewhere between 1/13.5 and 1/16.6.

A far better estimate because the number of observed successes is a lot higher. Let’s calculate the 95% interval for all the special cards:

Card	Pull Rate*	95% CI		Range
Palkia	1/846	0.0005	0.0026	1/2000	1/385
Arceus	1/635	0.0008	0.0031	1/1250	1/323
Dialga	1/423	0.0014	0.0041	1/714	1/244
Giratina	1/423	0.0014	0.0041	1/714	1/244
Mewtwo	1/242	0.0027	0.0063	1/370	1/159
Darkrai	1/423	0.0014	0.0041	1/714	1/244
Leafeon	1/452	0.0012	0.0039	1/833	1/256
Regigigas	1/423	0.0014	0.0041	1/714	1/244
Zoroark	1/317	0.0019	0.0051	1/526	1/196
Suicune	1/203	0.0033	0.0073	1/303	1/137

• Fun fact #1: All gold cards overlap between 1/714 and 1/385
  – This means gold card pull rate could not be shown to be significantly different
• Fun fact #2: All VSTAR cards overlap between 1/370 and 1/256
  – This means VSTAR pull rate could not be shown to be significantly different
• Fun fact #3: All gold cards and VSTAR cards overlap between 1/370 and 1/385
  – This means gold cards and VSTAR pull rate could not be shown to be significantly different LOL

The TL;DR is that based on the data, the true pull rate between any individual gold cards and VSTAR could all be the same. The infographic is virtually uninformative yet it’s easy to leave with a very different impression. Here is a new-and-improved version of the pull rates.

Let’s be reasonable though. We can pull something informative from this by making simple assumptions. Let’s assume the pull rate across all gold cards are the same. And let’s assume the VSTAR also have a consistent pull rate. It’s not crazy to think since ultimately these cards are coming from sheets which will have a mostly uniform distribution of each card of the same rarity.

6+8+12+12 = 38 gold cards pulled
Which means the pull rate is somewhere between 1/97 - 1/182

21+12+11+12+16 = 72 VSTARs pulled
Which means the pull rate is somewhere between 1/56 - 1/89

This is evidence that the two types of cards actually have different pull rates (possibly due to there just being more different kinds of VSTAR). Either way, these ranges are a lot more meaningful. You have to buy ~150 packs to see a gold card and ~70 to see one of the VSTAR

---

There you go. Don’t trust these infographics at face-value. Appropriate estimations for exact cards require 10x the data than what’s given here - closer to 50,000 packs. That being said, you can still use these graphics to get a general idea of the pull rate across a class of cards

---

1. yes, 11.2, we will round down to 11 ↩︎

2. ie. opening a pack ↩︎

3. ie. card pulled ↩︎

4. ie. card not pulled ↩︎

5. this is the one I will use Epitools - Calculate confidence limits for a sample prop ... ↩︎

6. note that 0.00118 is in this range ↩︎

[gengarbrigade]

@pfm I ain’t gonna lie, if you were a professor at the University of North Texas, I’d take the course just because to get an ounce of your brain. Well done.

[admiral]

[lyleberr]

Thank you for doing this. I was annoyed at the smaller amount of packs (usually its at least 10k) and noticed the same things you were seeing. General trends take time and the morning of official release with barely a week worth of limited prerelease and scattered data points isnt enough time to see the real rates.

[pfm]

I was trying to make this as accessible as possible and if this is the first response, I think I failed haha

[dack]

indubitably

[smokemon]

Forgive me if I glossed over what I’m going to ask, but when we say number of packs, does it matter if it’s from an ETB, single booster blister/hanging pack, or booster box?

Taking the booster box for instance, the way I understand it is you have only maybe 2 or so shots to pull the rarest cards from the set. Since the other 34 packs will not have the chance of hitting the rares, would the statistics be more favorable if they were from an etb or single pack?

Maybe I’m looking too deep here, but do you have a wider chance of pulling the rarest cards from multiple etbs vs. multiple booster boxes where the number of packs are the same?

[pfm]

The TL;DR is that the estimation of pull rate has a margin of error that is never shown in these infographics. The more packs you open, the more accurate the number is.

If you account for randomness, this shows the pull rate of each card with 95% confidence:

You will notice that the range is very big.

[TCGFish]

I somehow understand this. very good explanation.

from my understanding, this basically means, for the above cards = just buy singles = save money

[pfm]

If you open 4 booster boxes you can probably expect 1 gold card. But if you’re lucky you can pull up to 4. If you’re unlucky you could get zero

If you open the same packs via ETB (18 of them), you should also expect ~1 gold card. But if you’re extremely lucky you could get 18, one in each box. But there’s also a very good chance you get 0.

Both booster boxes and ETB should have the same “expected” pull rate. You’ll hit that expectation far more consistently with booster boxes. With ETBs, there’s more randomness so you’re more likely to have good luck and beat the expectation but at the same time, you’re also more likely to have bad luck and fall short of the expectation. So if you enjoy a higher risk/reward, ETBs are a better choice

[gengarbrigade]

LMAO

[camrok37]

This is the content I came to E4 for. I feel like I just sat through a free Pokemon masterclass. Bravo, good Sir, bravo.

[ascendedbidoof]

Thanks for putting this together! This really helped me understand why these are so misleading. It’s crazy to me that 5000 packs isn’t enough of a sample size to get a good understanding of the pull rates from just one set.

[needszeebs]

love to see some statistical analysis.

@pfm

This means we are pretty confident that the true pull rate for Palkia is somewhere between 1/2000 and 1/385.

this range is huge LOL would you have to run an ANOVA on all of the mean pull-rates for the gold cards to test for statistical significance? or can you just compare the confidence intervals? im still a stats student, but i find this stuff to be very interesting

[pfm]

Comparing confidence intervals like I did here is probably more intuitive than robust. A more proper way would be to calculate some kind of p-value. If you were comparing two cards pull rates, you could do a basic hypothesis test where p₁=p₂ and calculate z-scores, etc etc (but you have to assume the distributions are independent which they probably aren’t)

I haven’t done ANOVA since STATS101 but if I remember correctly it’s basically a similar test but focused on variance instead of mean and also works on multiple groups (but iirc if any one group is different, the null is rejected). I guess that’s more appropriate.

If I were really trying to be robust, I’d probably look at some non-parametric test since the independence assumption is being violated so I would not be comfortable assuming anything about the actual distribution.

All this being said, stats are not my specialty so while I understand many of the concepts, I’d defer to someone with an actual degree in Statistics

[Dyl]

You can compare the proportions with a Chi-Square test.

[fourthstartcg]

Yeah, from my very basic social science statistics background, ANOVA would technically be better suited here to determine with certainty whether any of the pull rates differ significantly from the other. But I highly doubt you would be able to get any result with such a small sample size like what we have here, even if the pull rates actually are different.

[Dyl]

We would not use an ANOVA here because we don’t have means. We have proportions. Our choices are a 2-sample test for the equality of proportions (z) or a Chi-Square test. Both will result in the same p-value.

[pfm]

But they both assume independence right?

[Dyl]

Yes, that is correct.